Embeddingについて Part1

入力データを低次元に特徴を埋め込むモデル構築に、最近私は取り組む機会が多くなっています。黙々と構築してきましたが、embeddingの良さをどのように測るべきか、ちゃんと厳密に考えていなかったなと痛感しています。モデルをさらに「改善」したいと思った時に、この改善ってどういうこと？となってしまいます。

感覚としては、モデルができるだけ多くの情報を埋め込む事が出来れば良いモデルとなりますが、それを確かめるためにはどうするべきでしょうか。

Autoencoderベースのモデルだと、再構築された出力から、入力データと比べることによってembeddingの情報量を調べる事ができます。

でももしAutoencoderから、LSTM+Autoencoderで時系列も考慮！みたいな改良を行なったとすると、後者は本当に改善したembeddingベクトルを生み出すのだろうか。再構築された出力結果を調べるだけでなく、embeddingベクトルの性質をみる必要があると思います。例えば、予測モデルの特徴量として活用して、精度が上がるかどうかなど。また、多数の予測モデルで多目的な予測の精度を確かめるなどすると良さそうだなと感じます。他には、クラスタリングなども使えそうですね。

embeddingモデルを構築したということは、何かの目的があり構築したはずなので、その目的を達するために改善したか測る方法を確立すると後々便利だなと感じております。

この記事は私の意見も入り混じっているので、何か色々とご意見をいただけると幸いです。

URLNetについてのお話

URL Embeddingについて書かれた論文を紹介します。紹介する論文は

「URLNet: Learning a URL Representation with Deep Learning for Malicious URL Detection」（Hung Le et al., 2018） Link: https://arxiv.org/pdf/1802.03162.pd

URL（文字列表現）を数値ベクトルの形式で表現する手法を紹介しています。

お馴染みのword2vecでのembeddingとは異なる点があります。教師あり学習で、目的にあったembeddingを実現させます。論文で使われている応用例が、不正なサイトに飛ばず悪質なURLかどうかを見分けるためにembeddingが使われています。

問題の設定

与えられているURLが悪質かどうかを分類する、分類器を構築します。教師あり学習なのでデータはURL（feature)とラベル(target)のペアとなり、ラベルが１だと悪質、−１だと悪質でないことになります。$T$個のペアがモデル構築に使用されます

$$\{(u_1, y_1), ..., (u_T, y_T)\}$$

 $u_j$がURL、$y_j$がラベルで、$y_j = +1$または$y_j=-1$となります。

モデル全体像

                                 

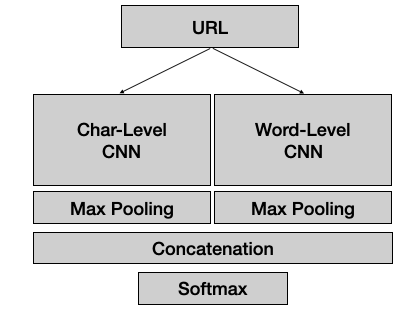
ざっくりになってしまいますが

1. URLがインプットされ
2. 畳み込み層（CNN）を通り
3. Poolingで次元を一次元ベクトルに次元削減
4. ベクトルを連結（ここの層から出力されるベクトルがURL Embeddingです）
5. 最後にsoftmax層の出力結果が分類に使われる

今回は以下の要点をみていきたいです。

URLをCNNに入れるためは？Char-Level CNNとWord-Level CNNの違いは？

まずはChar-Level CNNからみていきましょう。

Char-Level CNN

URL→toknize→char id→embedding matrix

embedding matrixがCNN層に入ることになります。

URLがhttps://www.hatena.ne.pjだとすると、

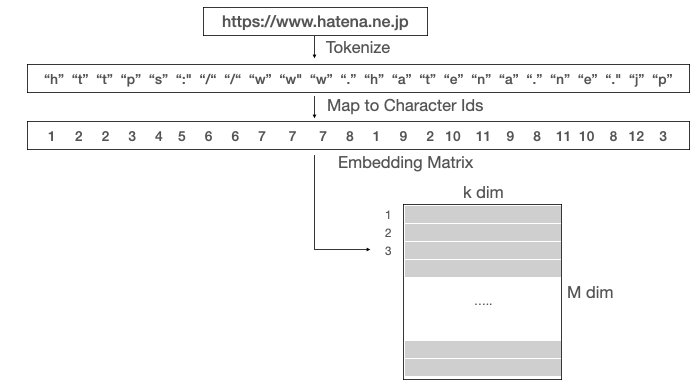
各文字を一意となるIDで表現し、またそのIDが行列（Embedding Matrix)のどの行を使うか指定します。入力されるURLの文字数は自由ですが、内部では必ず200文字になるように設定されます。

200文字未満の場合、補完が行われます。

例えば、www.hatena.ne.jp<PAD><PAD><PAD><PAD>・・・<PAD>

補完専用の文字ID＜PAD>を用意して、行列の特定の行を指定するようになります。

200文字を超える場合、200文字以内の文字のみ考慮されます。 

Embedding matrixの初期値はランダムに生成されますがbackpropagationにより数値が調整されます。

Word-Level CNN

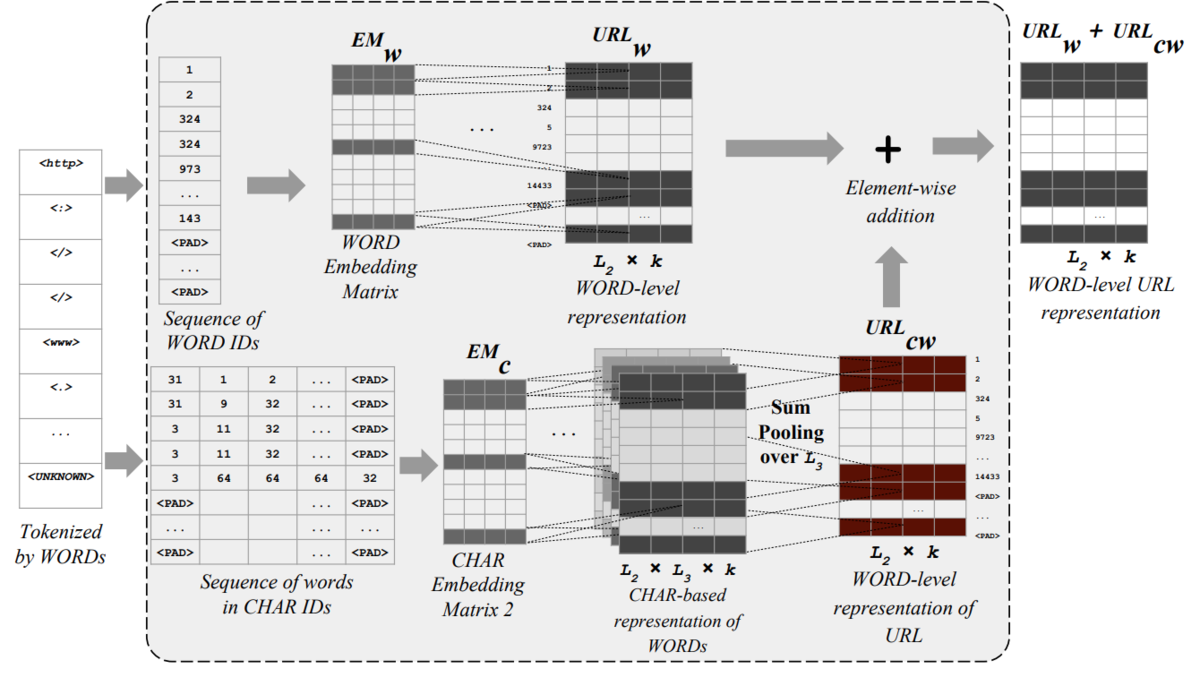
上の図をhatenaを例にみてみます。

　　　　　　　

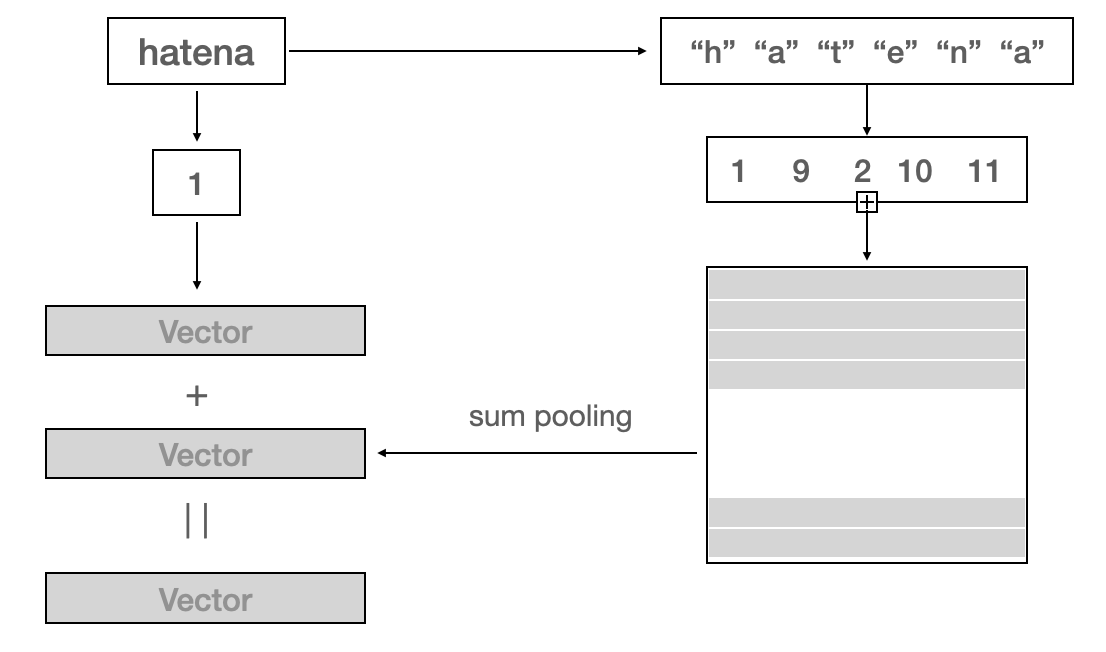
hatenaをベクトルで表現するために、Hatenaをword ID＝１で指定されたベクトルと、Hatenaの各文字のベクトルを足し合わせた表現、二つのベクトルを足し合わせることによって算出されます。URLの場合だと、各単語にこのやり方が適用されるので、URLから行列の表現に変換されCNN層に入り込むことになります。

単語を文字ベースでベクトル化することによって、モデルがみたことのない単語が入力された場合でもベクトル化が可能になります。（単語ベースのベクトルはゼロとされる）

うまくまとめる事が出来ませんでしたが、次回はもう少し頑張るようにします ^^ 

交差エントロピーに繋がるお話

機械学習でよく使われる損失関数。

エントロピー（Entropy）

1948年にShannonによって書かれた論文 (A Mathematical Theory of Communication)

http://people.math.harvard.edu/~ctm/home/text/others/shannon/entropy/entropy.pdf

10ページに以下の文章が書かれています

n個の事象（イベント）が起きる確率を$p_1, p_2, ..., p_n$。わかることがそれだけだとする。不確実性を示す尺度を見つけることができるだろうか？

 例えば、

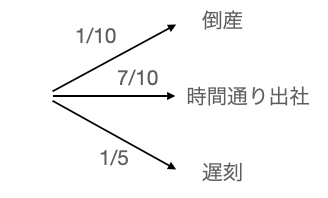
三つのイベント、（倒産、時間通り出社、遅刻）があり、起きる確率が$(1/10, 7/10, 1/5)$とし、足し合わせると1になります。上記の図は、同等に以下のようにも表現できます

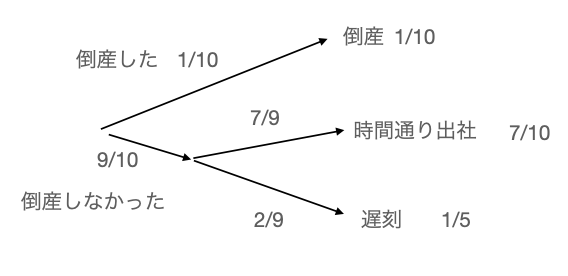
 倒産をしなかったから時間通りに出社、または遅刻、といった表現もできるので、上記に図に沿って計算すると同じ確率が算出されます

時間通り出社 = (9/10) x (7/9) = 7/10

遅刻 = (9/10) x (2/9) = 1/5

そして、このような同等の表現に不変であるべき尺度を$H$と書きますと、最初の例を

$H(\frac{1}{10}, \frac{7}{10}, \frac{1}{5})$

 ２番目の例を

$H(\frac{1}{10}, \frac{9}{10}) + \frac{9}{10} H(\frac{7}{9}, \frac{2}{9})$

 （$\frac{9}{10}$の確率が係数として使われる）

とすると以下の等式

$$H(\frac{1}{10}, \frac{7}{10}, \frac{1}{5}) = H(\frac{1}{10}, \frac{9}{10}) + \frac{9}{10} H(\frac{7}{9}, \frac{2}{9})$$

 を満たす$H$はなんでしょうか。

それが、よく目にするエントロピーの公式

$$H(p_1, p_2, .., p_n) = -\sum_{j = 1}^{n}p_j\log p_j$$

実際に計算をしてみますと、

$$H(\frac{1}{10}, \frac{7}{10}, \frac{1}{5}) = -\frac{1}{10}\log(\frac{1}{10}) - \frac{7}{10}\log(\frac{7}{10}) - \frac{1}{5}\log(\frac{1}{5})$$

 $$H(\frac{1}{10}, \frac{9}{10}) + \frac{9}{10} H(\frac{7}{9}, \frac{2}{9}) = -\frac{1}{10}\log(\frac{1}{10}) - \frac{9}{10}\log(\frac{9}{10}) -\frac{7}{10}\log(\frac{7}{9}) - \frac{1}{5}\log(\frac{2}{9})$$

$$=-\frac{1}{10}\log(\frac{1}{10}) - \log(9/10)^{9/10}(7/9)^{7/10}(2/9)^{1/5}$$

$$=-\frac{1}{10}\log(\frac{1}{10}) - \log(9/10)^{7/10}(7/9)^{7/10}(9/10)^{1/5}(2/9)^{1/5}$$

$$=-\frac{1}{10}\log(\frac{1}{10}) - \log(7/10)^{7/10}(1/5)^{1/5}$$

$$=-\frac{1}{10}\log(\frac{1}{10}) - \frac{7}{10}\log(\frac{7}{10}) - \frac{1}{5}\log(\frac{1}{5}) =H(\frac{1}{10}, \frac{7}{10}, \frac{1}{5})$$

 見事一致します。

結果イベントの確率のみで一意に表現できる尺度になっております。

そして、不確実性を示す量として適していることが以下の例でみられます。

$$H(p) = - p \log p - (1-p) \log(1-p)$$

 $p$はイベントの確率を示しております。グラフにすると

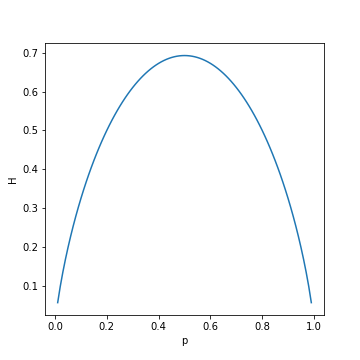
 $p=1/2$の値で頂点を達しているのがみられます。$p=1/5$の場合は、一番不確実であるとエントロピーの量からもみられます。

異なる確率を比較するための量は？

 カルバック・ライブラー情報量（Kullback-Leibler divergence)

Shannon氏の出版後に、まもなくKullback&Leibler氏が情報量に関して論文を出します。（On Information and Sufficiency）

Kullback , Leibler : On Information and Sufficiency

確率変数$X$が状態$x_j$である確率を$p_j$とし、$\sum_j^np_j = 1$を満たします。一方、別の確率$q_j$も、確率変数$X$が状態$x_j$である確率を$q_j$とし、$\sum_j^nq_j = 1$を満たします。

カルバック・ライブラー情報量とは、確率の差異を測る量になります。

$$\sum_{j=1}^n p_j \log\left(\frac{p_j}{q_j}\right)$$

実際に数値をみてみると

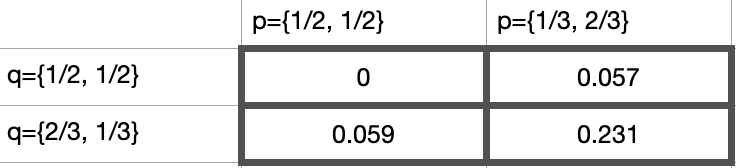
最小値は$0$で差異がない場合($p={1/2, 1/2}$, $q={1/2, 1/2}$)

最大値は$0.231$で確率の差異が一番大きい場合に起きる事がわかります。

では交差エントロピーとは？

交差エントロピー

 真の確率を$p$とします。推定した確率を$q$とします。交差エントロピーは以下で表現されます。

$$-\sum_{j}^{n}p_j\log(q_j)$$

エントロピーとカルバック・ライブラー (KL) を足し合わせることによって表現出来ます。

[交差エントロピー] = [真の確率pのエントロピー] + [pとqのKL情報量] 

$$-\sum_{j}^{n}p_j\log(q_j) = -\sum_j^np_j\log(p_j) + \sum_j^np_j\log\left(\frac{p_j}{q_j}\right)$$

 [真の確率pのエントロピー]はpの情報量を示しており、交差エントロピーに潜むそもそもの大きさになります。そして、$p$と$q$の差異をカルバック・ライブラー情報量で表現される事が出来ます。

実際に損失関数として使用されている形では、全てのサンプルに交差エントロピーを計算する必要がありますので、以下の形になります。

$$-\frac{1}{N}\sum_{k}^N\sum_{j}^np_{j,k}\log(q_{j, k})$$

$N$がサンプル数を示します。

Adamについてのお話

記念すべき第一回目の投稿です。

私、現在データサイエンティストとして、e-commerce系の大手会社で勤めております。

機械学習系のブログや数多くのリソースが増え知見を得ることが簡単になっています。私自身、web上で検索して数多くの知見を得ることができました。例えば、「ランダムフォーレストとは」と検索するだけで、分かりやすく解説をするブログに出会すことがあります。場合によっては、本を見つけて読むよりも、効率的かもしれません。論文を読みつつ、その論文を解釈する誰かのブログを読むことによって、“一緒に”論文を読んでいる気分になったりもしました。私自身ブログを始めるべきかどうか長い間考えた結果、始めることにしました。役に立つアイデア、理論、実験結果など共有したいことがあるからです。またこれからも沢山出てくるはずです。

役に立ったと感じた事、基礎的な事、面白いと思った事、を共有していきますのでよろしくお願いいたします！

いきなりですが Adamについて。（なぜAdam??ふと、今思ったからです…こんな感じで更新していきます。）

ADAMについて

 深層学習の最適法の一つして発明された手法Adam。2014年12月に投稿されすでに引用数が6万越え（現在2021年1月）。

https://arxiv.org/pdf/1412.6980.pdf

論文に記載されているアルゴリズムの部分

ハイパーパラメータとなるのは

$\alpha$ : 学習率

$\beta_1, \beta_2$ : 平滑化移動平均のために

$\epsilon$ : ゼロによる分割を防ぐために

そしてモデルのパラメータを$\theta$とすると、最小化したい関数を$f(\theta)$とします。

1. 初期ステップ$t=0$に変数を初期化 ($\theta_0=0, m_0 =0, v_0 =0$)。また、ランダムにデータをサンプルして、勾配$\nabla_{\theta}f(\theta)$を計算できる状態にします。
2. ステップのアップデートを行います。$t \rightarrow t + 1$
3. 勾配の計算$\nabla_{\theta}f_t(\theta_{t-1})$（これを$g_t$をとします）
4. 次に$m_t$のアップデート。これは$\beta_1$により、$m_{t-1}$と$g_t$の平滑化平均をとります。
5. 次に$v_t$のアップデート。これは$\beta_2$により、$v_{t-1}$と$g_t^2$の平滑化平均をとります。（$g_t^2$とは$g_t$の二乗）
6. 初期値（$m_0=0, v_0=0$）によりゼロにバイアスがかかってしまうので、$\hat{m}_t$と$\hat{v}_t$を計算することによって調節します。結果的に、$t=1$の場合だと、$\hat{m}_1=g_1$となります。
7. 最後に、パラメータ$\theta_t$のアップデートを行います。
8. $\theta_t$が収束するまでステップ2~6を繰り返します。

$v_t$は学習率を変化させる役割を担います。例えば、$v_t$が大きい場合、学習率が小さくなり急激な変化を妨げます。一方、$v_t$が小さい場合、学習率が大きくなり変化を大きくします。

 $\beta_1$と$\beta_2$はどうでしょうか。

$\beta_1$が$1$に近い場合、最新の勾配$g_t$の影響が小さいため、$m_t$の変化が激しくないことが予想されます。一方、$\beta_1$が$0$に近い場合、最新の勾配の影響が大きく考慮されるので、$m_t$の変化が激しくなりやすいことが予想されます。

同じ議論が$\beta_2$の場合にも適用することができます。

厳密ではないことを言ってしまいますが、$\beta_1$と$\beta_2$が$1$に近いと、安定した学習を可能とするのではないのでしょうか。

 Tensorflowで実験

TensorflowのAdamでも理論通りパラメータを取り入れます。

opt = keras.optimizers.Adam(learning_rate=0.001,
                            beta_1=0.9, beta_2=0.999,
                            epsilon=1e-07)

 MNISTのデータセットで簡単なANN分類器を構築し、二つのパターンの$\{\beta_1=0.9, \beta_2=0.999\}$と$\{\beta_1=0.1, \beta_2=0.1\}$を試した結果。

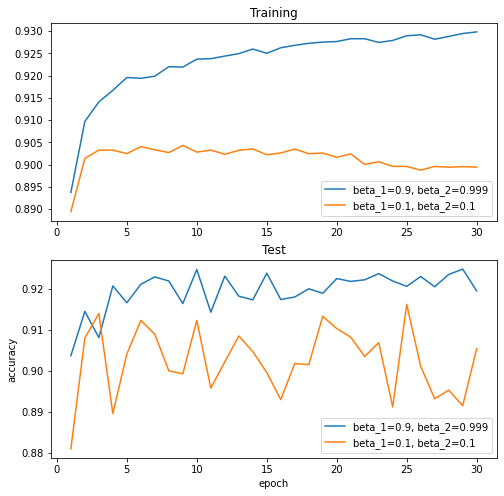
今回の場合、青の曲線$\{\beta_1=0.9, \beta_2=0.999\}$の場合の方が良いことが見られました。