交差エントロピーに繋がるお話

機械学習でよく使われる損失関数。

エントロピー（Entropy）
カルバック・ライブラー情報量（Kullback-Leibler divergence)
交差エントロピー

エントロピー（Entropy）

1948年にShannonによって書かれた論文 (A Mathematical Theory of Communication)

http://people.math.harvard.edu/~ctm/home/text/others/shannon/entropy/entropy.pdf

10ページに以下の文章が書かれています

f:id:shimaby:20210116200752p:plain

n個の事象（イベント）が起きる確率を$p_1, p_2, ..., p_n$。わかることがそれだけだとする。不確実性を示す尺度を見つけることができるだろうか？

例えば、

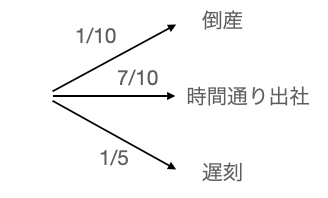
f:id:shimaby:20210116203819p:plain

三つのイベント、（倒産、時間通り出社、遅刻）があり、起きる確率が$(1/10, 7/10, 1/5)$とし、足し合わせると1になります。上記の図は、同等に以下のようにも表現できます

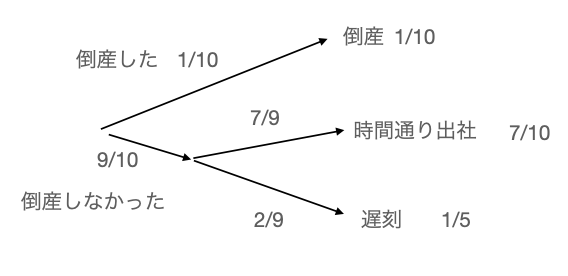
f:id:shimaby:20210116205101p:plain

倒産をしなかったから時間通りに出社、または遅刻、といった表現もできるので、上記に図に沿って計算すると同じ確率が算出されます

時間通り出社 = (9/10) x (7/9) = 7/10

遅刻 = (9/10) x (2/9) = 1/5

そして、このような同等の表現に不変であるべき尺度を$H$と書きますと、最初の例を

$H(\frac{1}{10}, \frac{7}{10}, \frac{1}{5})$

２番目の例を

$H(\frac{1}{10}, \frac{9}{10}) + \frac{9}{10} H(\frac{7}{9}, \frac{2}{9})$

（$\frac{9}{10}$の確率が係数として使われる）

とすると以下の等式

$$H(\frac{1}{10}, \frac{7}{10}, \frac{1}{5}) = H(\frac{1}{10}, \frac{9}{10}) + \frac{9}{10} H(\frac{7}{9}, \frac{2}{9})$$

を満たす$H$はなんでしょうか。

それが、よく目にするエントロピーの公式

$$H(p_1, p_2, .., p_n) = -\sum_{j = 1}^{n}p_j\log p_j$$

実際に計算をしてみますと、

$$H(\frac{1}{10}, \frac{7}{10}, \frac{1}{5}) = -\frac{1}{10}\log(\frac{1}{10}) - \frac{7}{10}\log(\frac{7}{10}) - \frac{1}{5}\log(\frac{1}{5})$$

$$H(\frac{1}{10}, \frac{9}{10}) + \frac{9}{10} H(\frac{7}{9}, \frac{2}{9}) = -\frac{1}{10}\log(\frac{1}{10}) - \frac{9}{10}\log(\frac{9}{10}) -\frac{7}{10}\log(\frac{7}{9}) - \frac{1}{5}\log(\frac{2}{9})$$

$$=-\frac{1}{10}\log(\frac{1}{10}) - \log(9/10)^{9/10}(7/9)^{7/10}(2/9)^{1/5}$$

$$=-\frac{1}{10}\log(\frac{1}{10}) - \log(9/10)^{7/10}(7/9)^{7/10}(9/10)^{1/5}(2/9)^{1/5}$$

$$=-\frac{1}{10}\log(\frac{1}{10}) - \log(7/10)^{7/10}(1/5)^{1/5}$$

$$=-\frac{1}{10}\log(\frac{1}{10}) - \frac{7}{10}\log(\frac{7}{10}) - \frac{1}{5}\log(\frac{1}{5}) =H(\frac{1}{10}, \frac{7}{10}, \frac{1}{5})$$

見事一致します。

結果イベントの確率のみで一意に表現できる尺度になっております。

そして、不確実性を示す量として適していることが以下の例でみられます。

$$H(p) = - p \log p - (1-p) \log(1-p)$$

$p$はイベントの確率を示しております。グラフにすると

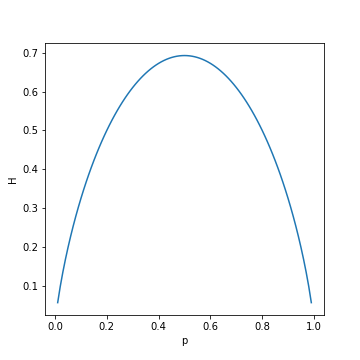
f:id:shimaby:20210116224104p:plain

$p=1/2$の値で頂点を達しているのがみられます。$p=1/5$の場合は、一番不確実であるとエントロピーの量からもみられます。

異なる確率を比較するための量は？

カルバック・ライブラー情報量（Kullback-Leibler divergence)

Shannon氏の出版後に、まもなくKullback&Leibler氏が情報量に関して論文を出します。（On Information and Sufficiency）

Kullback , Leibler : On Information and Sufficiency

f:id:shimaby:20210117161733p:plain

確率変数$X$が状態$x_j$である確率を$p_j$とし、$\sum_j^np_j = 1$を満たします。一方、別の確率$q_j$も、確率変数$X$が状態$x_j$である確率を$q_j$とし、$\sum_j^nq_j = 1$を満たします。

カルバック・ライブラー情報量とは、確率の差異を測る量になります。

$$\sum_{j=1}^n p_j \log\left(\frac{p_j}{q_j}\right)$$

実際に数値をみてみると

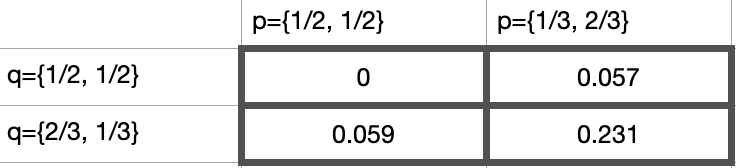
f:id:shimaby:20210117190624p:plain

最小値は$0$で差異がない場合($p={1/2, 1/2}$, $q={1/2, 1/2}$)

最大値は$0.231$で確率の差異が一番大きい場合に起きる事がわかります。

では交差エントロピーとは？